Goals for this homework

  • Practice with data representation, binary search trees, and heaps
  • Practice using compression techniques, encoding and decoding

You are expected to complete this assignment individually. If you need help, you are invited to come to office hours and/or ask questions on piazza. Clarification questions about the assignments may be asked publicly. Once you have specific bugs related to your code, make the posts private.

You should submit several files for this assignment ( compression.c, Makefile, and any associated testing files that you create) in your subversion repository as directed below.

Set Up

You should already have your set of files from the warmup. Make sure you copy over the files from your duet programming folder, if applicable.

You need to add the skeleton code so that your program will minimally execute. You must do this in case you do not complete your assignment. Our testing infrastructure needs to compile and execute even if you did not complete the entire assignment. Refer to past assignments on how to make skeleton code.

Overview

Our goal is to compress information that is handed to us in the form of a plain text file. Our output will be a string of pseudo-binary codes, comprised of the characters "0" and "1", representing each word in the text file. The process we will follow to do this is as follows:

  • Given a text file, use get_counts() from hw6 to build the first bst (sorted alphabetically)
  • Use iterate(bst *tree) from bst.h, build a new bst sorted by frequency
  • Create an empty heap with creation function from heap.h
  • Use a new function in compress.h build_compressionnode_heap(bst *tree) which will iterate through the frequency-sorted bst and wrap each wordcount struct in an encoding node, and insert each encoding node into the heap
  • Use build_encoding_tree(heap *hp) from compress.h which performs the encoding algorithm
  • Use record_codes(encodingTree *tree) from compress.h to iterate through the encoding tree struct and assign each codeword to the codeword attribute of the corresponding wordcount struct. This does not return anything, just modifies the corresponding wordcount structs and assigns the correct codes
  • Use the function encode(char* filename) to take in a file and split it into words, and for each word in the file write the corresponding codeword to a new file
  • Use decode(encodingTree* tree, char* filename) to take in our compressed file and output the appropriate decoded file, obtained by traversing the encoding tree according to the sequence of binary characters

    • Problem 1: Encode

    the goal

    Our goal in this problem is simple: given a text file, we want to assign a code to each word in the file such that we can satisfy two main criteria:

  • The encoded message can be decoded efficiently and uniquely, and
  • The compressed file is small
    • Specifically, we will be handed text files that are comprised of a sequence of words, and for each of these words we want to assign a unique code made of solely "0" and "1" characters to represent them, and replace them with these codes to create a compressed file.

    To do this, one natural solution would be to simply count the number of distinct words present in the file, and assign each one a unique code in binary that represents the ordering of the word. For instance, if there are 10 words in a text file, one could assign the first word the code 0000 , and the second word 0001 all the way to 1001 representing the last word (10 counting from 0).

    What if one word happens much more often than any other? In that case, it seems that we are wasting some space by assigning each word a fixed bitwidth size code. To take advantage of the frequency with which words show up in our files, we would like to use much shorter codes for words that occur more often, and we can save longer codewords for those words that occur less frequently.

    However, this immediately runs us into a problem: how will we differentiate between certain codewords if we can vary the length? For example, say our text file includes the words "the" "and" and "extravagant", and both "the" and "and" occur far more frequently than "extravagant". Let's say we use 0 to encode "the", 1 to encode "and", and 001 to encode "extravagant". Say we come across an encoded text file that reads 001001 . Is this file encoding "the the and the the and", "extravagant extravagant", or something else?

    In going to variable length codewords, we have lost our ability to decode messages uniquely. How are we going to fix this? Luckily for us, we know about binary trees, and we can come up with a way to put this to use!

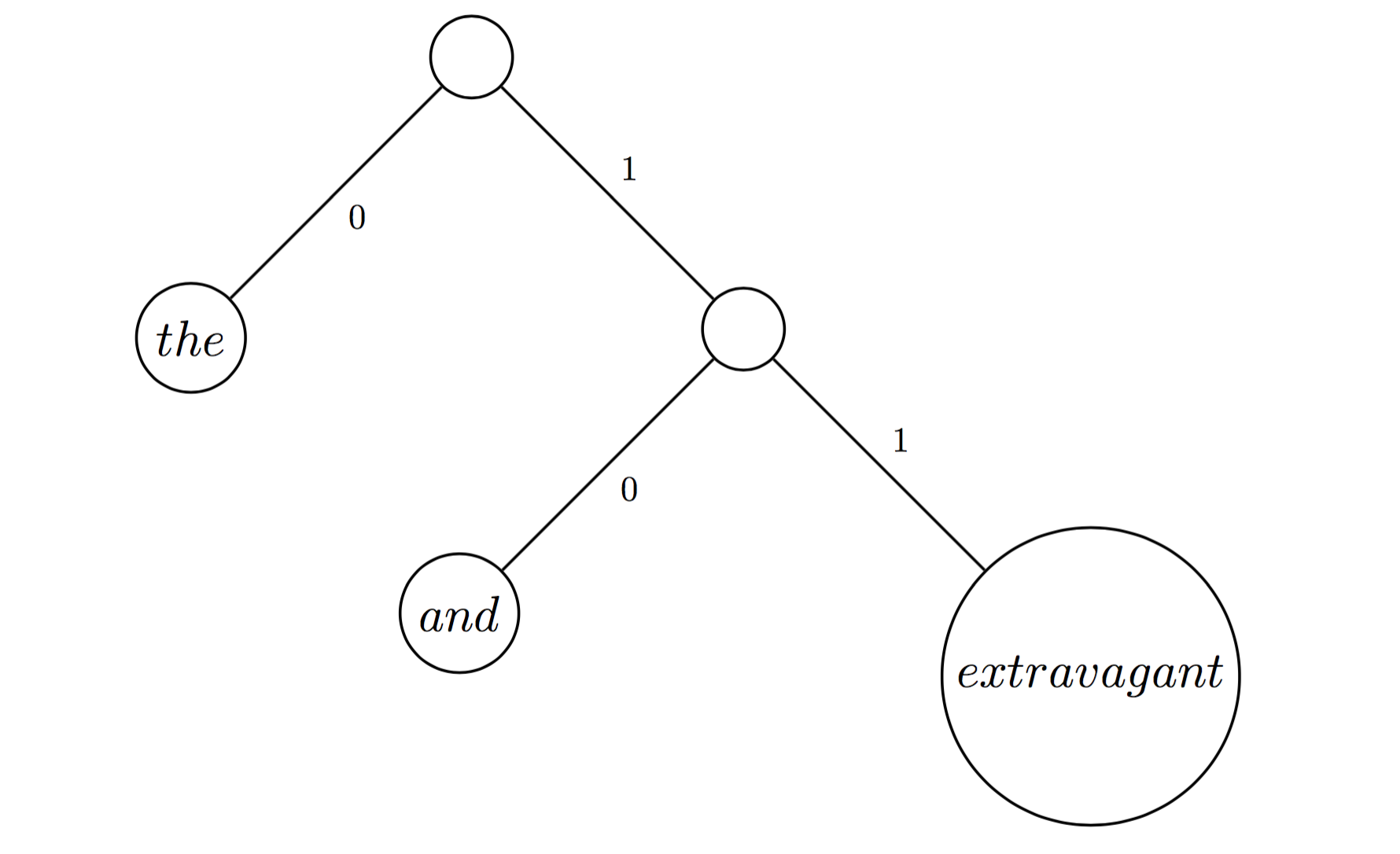
    Take a look at the following picture: Encoding Tree

    What we have here is a tree representing an encoding scheme for our three words, and the codes for each word are unique in that no codeword is a prefix of any other codeword. More specifically, we avoid our earlier trouble by avoiding exactly what caused the problem - one codeword was mistaken for another as it was contained in the prefix of another codeword itself. Here, notice that our codewords 0, 10, 11 are each unique in their prefixes. No one codeword can be mistaken for another. We call encoding schemes like this "prefix codes".

    The Algorithm

    In order to generate a tree like this, we want to make use of the fact that we know which words have the highest frequency, and in fact we know the entire ordering of the frequencies of all of the words in our text file. Our algorithm will work as follows:

  • We begin with all of our words and their frequencies, which we created by utilizing our earlier helper functions, in one list. We will consider this our list of one-leaf trees.
  • Next, we find the two words with the lowest frequencies, and combine them in a tree. In doing this, we create a new tree, and a new node with frequency equal to the sum of the two combined words. This new tree will have a newly constructed node that has a frequency that is equal to the sum of the two frequencies of the combined nodes. Of the two nodes we combined, the node with the lowest frequency is placed as the left child of the new node, while the other node is the right child.
  • Now, we go back to our earlier step, and operate on our new list. The list now contains all of the original words as one-node trees, and one more node that represents our combined words. We again combine the two nodes with the lowest frequencies. This could possibly combine our new combined-node with another word!
  • Continuing this process, our algorithm proceeds until there is only one node remaining. Then, we have found the root of our encoding tree.

    • Implementation

    Our implementation of this algorithm will use all of our helper functions that we completed in the warmup. Conceptually, we will be:

  • Creating a binary search tree of each of the words sorted by frequency
  • Wrap each of our wordcount structs from the tree in an encoding node struct
  • Creating a heap out of these encoding node structs, lowest frequency on top
  • Implementing our encoding algorithm by operating on the heap
  • Arriving at our ultimate goal - our encoding tree

    • The heap

    Our first step will be building an encoding tree, which is a binary search tree, sorted by frequency of the underlying wordcount structs. This can be performed by iterating through the alphabetically sorted bst and inserting each node into a new bst, using a compare function that compares frequencies.

    In building our heap from our frequency ordered bst, we will need to initially construct our compression tree:

  • Implement the heap_compare_counts function that distinguishes which of two encoding node structs has a higher frequency count
  • Use an iterator to visit each wordcount struct in the bst, and place each one into an encoding node
  • Insert each of these encoding nodes into our heap, using our heap compare function

    • It is important to note that the heap is implemented as an array, with the "top" of the heap represented by the first item in the array, and the "bottom" represented as the last element in the array. It can be viewed as a binary search tree that has been flattened by a level order traversal. 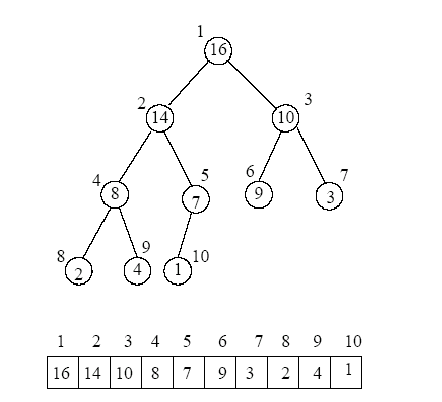It is most clearly seen in the below diagram, where a bst representation of a heap is mapped to an array: Heap as array

    We will be using exclusively the array representation of the heap to implement all of our functions.

    Once we have built our heap, the trick will be how to implement our algorithm utilizing this data structure.

    Using our comparison function that sorts by lowest frequency, we will obtain a heap that contains the lowest frequency count word first, which is a wordcount struct stored as an attribute of our encoding node struct. This facilitates our algorithm - now all that we must do is remove from the heap one element at a time, combine these encoding node structs into a new encoding node with left and right child node pointers to our original encoding nodes, and re-insert this new node and new frequency back into the heap. We will do this until our heap contains a single node. Once this process terminates, we will arrive at our goal - an encoding tree built from word frequencies!

    This process bullet pointed looks like:

  • Remove from the top of the heap (this will pull out the lowest frequency encoding node struct, and the heap will re-sort all items according to the heap property)
  • Remove again the top of the heap (getting us our two lowest frequency count encoding nodes
  • Combine these two encoding nodes by creating a new encoding node, and storing the sum of the two frequencies of the nodes we removed. The first node the heap gave us becomes the left child of the newly created encoding node, and the second node the heap gave becomes the right child
  • Insert the new node back into the heap which will re-sort
  • Repeat this process until the heap contains only one node

    • encoding

    Once we have our encoding tree, all that is left to do is to apply these new codewords to the words in our text file. To do this, we will use the following algorithm:

  • For each word in our text file, we will traverse the encoding tree to find it
  • At each edge, if we follow a left-edge, we add a "0" to our code
  • Or if we follow a right-edge, we add a "1" to our code
  • Once we arrive at our word, we return the accumulated codeword and the number of bits we accumulated, setting the appropriate attributes in the wordcount structs

    • For efficiency, once we build our encoding tree we will traverse the tree and save every word's associated codeword. In order to efficiently represent this, we can keep these codewords in one more binary search tree, sorted alphabetically. Just like our first binary search tree, this will allow us to quickly look up words we encounter when we are applying our encoding scheme. Instead of word counts, we will instead have a char array attribute corresponding to our codeword that was discovered in our encoding tree. This will be a fixed-width char array of 32 entries, (representing 32 possible bits), and a corresponding "bits" integer that will keep track of the actual size of the codeword for this specific word. With this information, we can read in a file, break it into words, look up each word in this bst, and output the corresponding codeword.

    Note: You will be outputting the string. You will not be responsible for packing those 1's and 0's into integers to out put more compactly. You will output the bit string.

    Problem 2: Decode

    The algorithm

    The goal here will be to use our encoding tree to decode an encoded file. This is much simpler than encoding, as we will have previously generated our encoding tree, and all we must do is traverse the encoding tree for each "bit" we read in from an encoded file. Each "bit" is a character '1' or '0' in the file. Once we arrive at a leaf node, we output the corresponding word, print out a space, reset our iterator, and keep reading!

    Extra Credit: Self-Balancing

    For extra credit, we can go ahead and implement our binary search trees as self-balancing. These are binary search trees that attempt to automatically keep their "height", or the number of levels (maximum number) below the root, as low as possible, and still responding properly to insertions and deletions.

    In order to receive credit, additional functions may be added to the bst.h, bst.c file enabling this functionality. For additional information, see (https://en.wikipedia.org/wiki/Self-balancing_binary_search_tree)

    Submit

    At this point, you should have done the following:
    • Created the file compress.c and any associated testing files you used, inside your hw7 director on subversion. Don't forget to add and commit everything you worked on!
    • Implemented all of your functions. If not, you at least need skeletons of your functions so that our automated tests will compile for the functions you did write.
    • Compiled your executable manually and with the Makefile
    • Implemented your test cases
    • Executed your code
    • Debugged your code 
    • $ svn commit -m "hw7 complete"