Due Wednesday, December 1 at 10pm.
This assignment should be done using the Advanced student language.
Write a function that maps a vector to a new vector
;; vector-map : (X -> Y) (vector X) -> (vector Y) (define (vector-map f v) ...) (check-expect (vector-map (lambda (x) (odd? x)) (vector 0 1 2 3)) (vector #f #t #f #t))
Using imperative data structures, we can build cyclic data structures. One such data structure is the representation of a double-ended queue (known as a deque) using a doubly-linked list.
A (deque X) is represented by a struct containing front and rear fields. For an empty deque, these fields will contain #f, otherwise they contain the first and last nodes of a doubly-linked list. The following data definitions are used to represent deques:
(define-struct deque (front ;; either a (deq-nd X) or #f rear)) ;; either a (deq-nd X) or #f (define-struct deq-nd (val ;; the node's value (type X) pred ;; the node's successor; either a deq-nd or #f succ)) ;; the node's predecessor; either a deq-nd or #f
The empty deque is represented as
(make-deque #f #f)
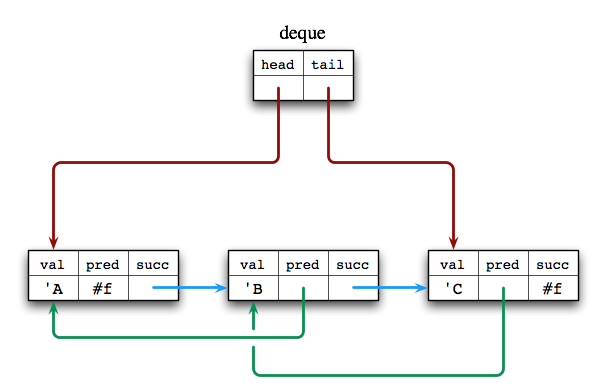
The following picture illustrates a deque with three elements ('A, 'B, and 'C). The first node contains the value 'A and the last node contains the value 'C.

Because deques are represented using cyclic structures, the update operations on them will be imperative. Recall that Scheme will generate the following destructive update operations from the define-structs for you:
;; set-deque-front! : (deque X) (deq-nd X) -> void ;; set-deque-rear! : (deque X) (deq-nd X) -> void ;; set-deq-nd-pred! : (deq-nd X) (oneof deq-nd #f) -> void ;; set-deq-nd-succ! : (deq-nd X) (oneof deq-nd #f) -> void
(a) Develop a function that lists the nodes in a deque. For example, called on the deque pictured above, it should return '(A B C). The function has the following header:
;; deque->list : (deque X) -> (list X) ;; returns a list of the items in deq in front to back order. (define (deque->list deq) ...)
(b) Develop a function to add an element to the front of a deque.
;; deque-push : (deque X) X -> void ;; push an item onto the front of the deque (define (deque-push deq item) ...)
(c) Develop a function to remove the first element of the deque.
;; deque-pop : (deque X) -> X ;; pop an item off of the front of the deque; returns #f if the ;; deque is empty (define (deque-pop deq) ...)
Note that for this function, you need to detect the case of a singleton deque and handle it specially.
(d) Develop a function to find and remove the first element of a deque that satisfies a given predicate.
;; deque-find-and-remove : (X -> boolean) (deque X) -> (oneof X #f) ;; find the first element of the deque that satisfies the predicate and ;; remove it from the deque. Return the removed item or else #f if there ;; is no item satisfying the predicate. (define (find-and-remove pred? deq) ...)