Com Sci 222/322
Machine Organization

Lectures

Chapter 2: Instruction Set Principles and Examples

Department of Computer Science
The University of Chicago

Last modified: Mon Feb 2 11:49:32 CST

Reading guide

Chapter 2 is fairly dense with interesting technical information, and the whole thing is worth a close reading. Because time is tight, we will focus on 2.2, excerpt 2.3, focus on 2.4, skim 2.5-2.6, rework 2.7, and focus again on 2.8-2.9. 2.8 will be left mainly to your independent reading, and lectures will emphasize 2.2-2.4, 2.7, 2.9. Read 2.10 quickly for stimulating ideas, but don't worry if some or most of the ideas are unfamiliar. Read 2.11 for fun.

When reading this chapter, be aware that Patterson is a key inventor of RISC (Reduced Instruction Set Computer) ideas. He discusses the RISC idea explicitly in Appendix C, but the RISC ideology probably affects Chapter 2 implicitly as well. I don't find anything misleading, but some ideas might have been structured a bit differently by someone who is not a proponent of RISC. In particular, the comparison with VAX instruction set in 2.8 suggests VAX as a natural opposite to RISC. But, another analysis might suggest that VAX was not the right non-RISC architecture to compare. One might use more sophisticated instructions than RISC does, but choose very general-purpose instructions, rather than the fairly specialized ones in the VAX. Or, it may be that the success of RISC has more to do with leaving room for lots of general-purpose registers than with the instruction set itself. At some point, there may be room on a CPU chip for sophisticated instructions and ample registers.

Memory in the CPU

Read 2.2 carefully.

A key architectural issue is the extent to which a modest amount of very high-speed memory should be located very close to the CPU (with modern VLSI, on the same chip), and how that memory should be organized. The text presents the possibilities quite well. A few extra points to notice:

• An accumulator is really just a register. ``Accumulator'' architecture is essentially 1-register architecture. Control of the CPU dataflow is simplified a lot by having just one register, and instructions are shorter. But, with only one register, one operand for a binary operation must come from main memory. With multiple registers, all operands may come from registers.
• The stack mentioned here is a stack of single words, used to hold operands for expression evaluation. It is treated differently from the recursion stack, which holds larger and variable-sized frames containing all the local variables to a procedure invocation. A stack architecture has a modest number of memory words in the CPU, organized as a stack. When the in-CPU stack overflows, its bottom is written out to main memory; when the in-CPU stack POPs, it may be refilled from main memory. This traffic between in-CPU stack and memory is handled automatically without execution of any extra program instructions. In principle, the stack is treated as a special sort of cache, although the design problems have little to do with those in modern caches.
• General-purpose registers and accumulators, unlike the stack, interact with main memory only through explicit LOAD and STORE instructions.
• A variety of special-purpose registers used to be popular, including registers to hold addresses vs. registers to hold numerical values. Modern architectures tend to prefer the largest possible number of general-purpose registers. But, there is still a tendency to provide special floating-point registers, presumably because of the special circuitry to separate mantissa from exponent.

In principle, cache is another form of in-CPU memory. It isn't mentioned here, because it is generally conceived as a buffer improving the performance of communication with the main memory, rather than as another CPU resource. Is it possible that cache will replace general-purpose registers in the future? Think about this possiblity when you read about register allocation in compilers in 2.7, and again when you study cache memory in Chapter 5. Set a mental flag to think about cache in connection with context switching---the saving and restoration of register contents for procedure calls/returns and scheduling of parallel processes (sometimes called coroutines). Also ponder whether there is waste in LOAD and STORE instructions when they work through a cache.

Assembly/machine language programs are almost always presented in a rather ugly and hard-to-read syntax, as in the ``Example instructions'' column of Figure 2.5 p. 75. To understand the computational result of a program, it is better to use a higher-level notation, such as that in the ``Meaning'' column of the figure, and to keep in mind that only a few of the natural assignment commands are actually allowed. To follow the instruction layout and other internal economic issues, the official ugly notation is better.

Forces in favor of lots of general purpose registers

The text correctly identifies a trend toward more and more high-speed registers in the CPU, and toward these registers being general purpose rather than specialized. Here are some forces pushing in that direction:

1. Improvements in VLSI fabrication produce more space on a chip. High-speed registers provide an easy (in the sense of design effort) way to take advantage of that space.
2. Compilers are very good at taking advantage of registers.
3. CPUs are speeding up more than memory access. Registers reduce the problem of memory bottleneck in two ways: they reduce traffic to memory, and they buffer the remaining traffic to even the load.

Memory addressiong modes

Read the first part of 2.3 carefully, through ``Addressing Modes'' on pp. 74-76. You may skip the rest.

I've never heard of a machine that addresses individual bits.

Make sure that you understand precisely what ``Big-Endian'' vs. ``Little-Endian'' addressing means. It's rather silly, but a fuzzy understanding of it can cause real serious and hard-to-debug errors. The names ``Big-Endian'' and ``Little-Endian'' come from the visit to Lilliput in Gulliver's Travels. Perhaps someone will post a summary of the relevant part of the story.

Make sure that you understand the precise meanings of the 10 main-memory/register addressing modes in Figure 2.5, and their uses. Figure 2.5 is a bit confusing, because it doesn't say which of the several addresses in each example illustrates the mode in question. Also, the names of modes sometimes mention the location being referenced and sometimes the location holding the address.Make sure that you resolve all the ambiguities.

6 of the modes are strictly ways of referencing a location in main memory. Register mode addresses a register, rather than using a register to address main memory. Immediate ``addressing'' really doesn't address anything in main memory or general-purpose registers: rather, it provides a constant value within an instruction. Since the instruction is stored in an instruction-decoding register in the CPU, you might argue that it addresses a field within that special register. Autoincrement/Autodecrement are combinations of referencing with a calculation to save an instruction. If you program in C, figure out how these addressing modes relate to C features. Why is incrementing done after addressing, but decrementing is done before addressing?

Notice that the different addressing modes can be applied to the result of an operation, as well as to its inputs. Particular instruction sets may provide different addressing modes in different instructions and different operand positions in the same instruction.

Simulating one addressing mode with another

For the theoretical functional requirements mentioned below, the direct addressing mode is sufficient, but the simulation of other modes is subtle and not practically sensible. The register mode can simulate all other modes in a direct and practically sensible way, but those simulations require additional instructions to load and/or store between registers and memory, and are therefore significantly costly. Finally, there are some simulations of one addressing mode by another that do not require any extra instructions, as long as appropriate constant values are already available in registers. These simulations can be quite attractive, and the simulatable modes are often omitted:

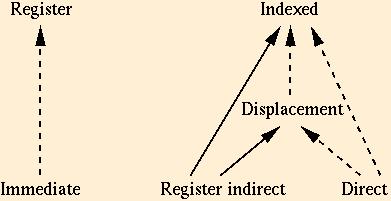
To be a good assembly language programmer, you must be very fluent in the relations between addressing modes, including the code size and performance issues.

The operations

The study of computer architecture imposes a particular performance-oriented point of view on the consideration of operations in the instruction set. I'll sketch some of the other points of view, to give a broader context.

The first requirement for an instruction set is that it provides a general-purpose computing system. This concept is a formal mathematical one, treated in theory courses. Essentially, it means that the instruction set must be capable of simulating all other computable instructions, given sufficient memory. The concept of ``computable'' has a formal mathematical definition, but there is some subtlety in the notion of ``sufficient memory.'' Although computer architects don't discuss this theoretical requirement explicitly, nobody has ever sold a computer that does not satisfy it, although it is easy for a naive person to propose insufficient sets of operations. Theoretical sufficiency is satisfied as long as we have addition, subtraction, and a conditional branch based on a zero-test. Registers (as opposed to main memory) and fancy addressing modes have nothing to do with theoretical sufficiency, they are there to improve performance.

Theoretical functional requirements and performance are both crucially important. It is always a mistake to ignore either one. But, it is useful to separate them, and to know which one is relevant to a particular architectural feature. There are different levels of importance in the performance issues, too. Some redundant operations may be simulated by a small fixed number of more primitive operations. For example, we may simulate an unconditional jump with a conditional branch whose condition has a fixed value. Other operations require a large sequence of more primitive operations, with the size growing due to surrounding context. Procedure calls (discussed below) are in this class. The latter case is usually crucially important to performance, while the former case is important only if the redundant operation is very common. To a great extent, the former case leads to issues of efficient encoding, as much as of speed.

Most operations, particularly those using the ALU, transform and move information around main memory and general-purpose registers. Jumps and branches are thought of as providing control flow for the memory-oriented operations. But, from a circuitry point of view, jumps are assignments of immediate values to the PC, and conditional branches provide a primitive way to transfer information from memory and general-purpose registers to the PC. Some instruction sets provide for computed jumps, which are assignments of arbitrary values to the PC. Why don't we absolutely need an instruction for transferring information from the PC to memory/registers? Instructions for procedure calls save the PC value, but they are there for performance, and not strictly essential to general-purpose computing.

While running a single program with no procedure calls and no modification of code, it is often useful to view the PC as the state of a Finite-State Machine (recall that we viewed the PC of a microcode interpreter in this way). In this view, the flow-chart for a program without procedure calls or self-modification is the transition diagram for an FSM, whose output is a sequence of operations on values in memory/registers. This view of program execution is quite valuable in the design of code generation in compilers. Procedure calls complicate the picture, but the bodies of individual procedures may often be understood through FSMs, even when the whole program may not.

Procedure calls provide a nice case study in the interplay between compilers and computer architecture. Procedure calls are not needed for theoretical sufficiency, but they make a big difference in performance, since the simulation of procedure calls requires an unlimited amount of inline substitution. Early architectures catered to nonrecursive procedure calls with a return jump operation transferring control to the procedure body, and saving a jump back to the calling code in the procedure body (usually at the beginning of the procedure rather than the end---try to figure out why). Return jumps were found to be insufficient for supporting recursive programs. At first, this was taken as a reason to avoid recursion, but later work worked on the assumption that recursion is useful, and must be made efficient. So, some architectures, such as the VAX, provided very powerful instructions catering to essentially everything that must be done in a procedure call, including stacking a return address, allocating local storage, saving/restoring register contents. Now, the VAX approach appears to be an over-reaction. Compilers can analyze the use of registers by procedures and the programs that call them, optimizing code for the actual use instead of covering all possible use. So, many current architectures have a procedure call instruction that allocates local storage on the recursion stack, but saves only the PC, leaving register saves and restores to explicit instructions generated by the compiler. If the use of parallel programming increases radically, how will this affect the architectural support for procedures?

The text does a nice job of describing the relative frequency of different sorts of operations, and the architectural implications. Pay close attention to this aspect of the text.

Forms of branching instructions

I find the explanation of branching instructions in Figure 2.14 on page 83 rather hard to understand. Here is how I've worked it out:

Condition Code (CC)

Each conditional branch involves two instructions.

1. The first instruction performs a test at the same time that it does an arithmetic operation. E.g., do a subtraction, and test whether the result is negative. The result of the test is stored in a special 1-bit register, called the CC register.
2. The second instruction is the branch itself. It branches according to the value in the CC register.

The two instructions are not required to be contiguous, but since there is only one CC register, there can be no other instruction that tests a condition between the two. I think that there may be architectures with a small number of CC registers for different types of condition.

Condition register

The name is misleading, since this method uses an arbitrary register, specified by the test instruction, instead of a specially reserved CC register. In effect, this method has a special-purpose branch instruction with only one branch test: branch on zero. It also has instructions that test other conditions (e.g., whether a value is positive), and assign 0 or 1 to a specified register depending on the truth or falsehood of the condition. Some such condition testers may defined arithmetically. For instance, equality test is just subtraction.

Compare and branch

This is the form that corresponds most closely to a conditional branch in a higher-level language. A single instruction tests a condition, and branches depending on the truth or falsehood of the condition.

Operation code economy

You can skim through 2.6. Notice that the use of varying-length instructions plus addressing limitations in jumps and branches leads to instruction alignment issues. These issues usually have to do with branches to an instruction, rather than the instruction's own action.

Interaction of architecture and compiling

The topic of 2.7 is crucial, but I am not completely satisfied with the text in this area. Read carefully on pp. 89-94, and relate the text to my extra comments below. Pp. 95-96 are rather general, and you can skim them.

• In Figure 2.19, Strength reduction and Pipeline scheduling are examples of peephole optimizations, since they may be performed by looking at a small number of contiguous instructions in a ``peephole'' that slides across the code.
• The phase order problem referred to in the text is a part of a general practical organizational problem facing compiler writers. Complete global optimization is too complicated to be practical: various parts of the program must be optimized independently, and various types of optimization must be carried out independently, even though the performance issues interact.
• Register allocation, emphasized several times in the text, is a very important part of the performance optimization done by compilers. In particular, the compiler is responsible for saving and restoring register values as necessary in procedure calls and returns. In principle, a register value only needs to be saved and restored on calling a procedure A from code B if A changes the register value, and also B needs that value again. Unfortunately, A and B usually need to be optimized independently. Depending on expected patterns of use, the caller save strategy saves all of the registers needed by B, or the callee save strategy saves all of the registers modified by A. In principle, only the intersection of these classes needs to be saved, but in practice it is usually too difficult to co-ordinate the information needed to find that intersection.
• When many procedures operate in parallel, it is practically infeasible to know what registers will be changed between times when a particular procedure runs. So, context switching for parallel procedures is particularly conservative about saving registers, and therefore relatively expensive.
• Heap-allocated variables are in essentially the same condition as local variables in parallel procedures, except that they are vulnerable even when there is no actual parallelism. Register allocation for these variables is usually too difficult, and they are written to main memory.
• From one point of view, a cache is a set of registers allocated by the hardware at run time. In principle, the use of cache instead of directly addressable registers might become more efficient than static allocation of registers by compilers. So far, the details have not worked out, and nobody is willing to give up general-purpose registers.

DLX

DLX is not a real machine, but it is very realistic, and there are simulators for it. We will probably have assignments in DLX assembly programming. Read 2.8 carefully and independently, making sure that you understand precisely what each instruction does. This is a better presentation of a machine language than you will find for real machines. Ask questions now if there are items that you don't understand.

Fallacies and pitfalls

Pay particular attention to the last two fallacies. These are connected to a common motivational pitfall that arises in essentially all realms of endeavor, not just computer architecture. People, particularly students, have a bad tendency to take one of two extreme and equally harmful attitudes:

• Failure is unacceptable, so I'd better not try.
• Failure doesn't matter, so I don't need to try.

odonnell@cs.uchicago.edu