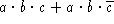Com Sci 222/322
Assignment #1
Winter 1999
Boolean arithmetic and circuits
Due Wednesday 13 January
In the future, we will try to hand in assignments online. Since the
pictures of combinational circuits in Assignment #1 may be difficult
to produce online, you may hand this one in on paper at the beginning
of class on Wednesday, 13 January. Please make the formulae and graphs
very neat and legible.
If you feel adventurous, you may submit your Assignment #1 by
electronic mail to odonnell@cs, by the end of the day on
Wednesday, 13 January. Please let the subject line be
CS222 Assignment #1 or CS322 Assignment #1,
appropriately. I will accept the following formats:
- highly readable plain text,
- Postscript.
I must be able to view your Postscript on the CS department's
Unix systems with the gv command. There are many ways
to produce Postscript, including proprietary word
processors. My own favorite is to use LaTeX for text and mathematics,
and xfig for pictures.
- Use truth tables to determine whether the following Boolean
expressions are equivalent:
-
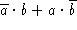 vs.
vs. 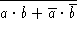
-
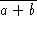 vs.
vs. 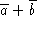
-
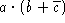 vs.
vs. 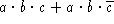
- Simplify the following Boolean expressions:
-
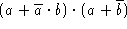
-
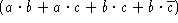
-
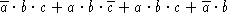
-
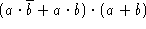
- Draw combinational circuit graphs for the unsimplified Boolean
expressions in problem 2, using and, or,
inverse.
- Draw combinational circuit graphs for the unsimplified Boolean
expressions in problem 2, using only binary multiplexors, and
extra inputs with the constant values 0 and 1. This is the sort
of circuit that can be implemented with mechanical relays.
- Draw a combinational circuit graph, using and, or,
inverse, with 3 inputs. The output must be 1 if and only if
precisely 1 or 3 of the inputs are 1.
- Draw a combinational
circuit graph, using binary multiplexors plus constant 0
and 1 with the same behavior.
- Convert the following circuit graphs to Boolean expressions, and
simplify:
-
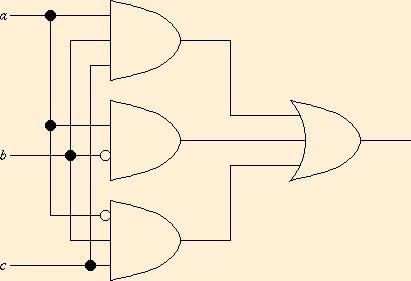
-
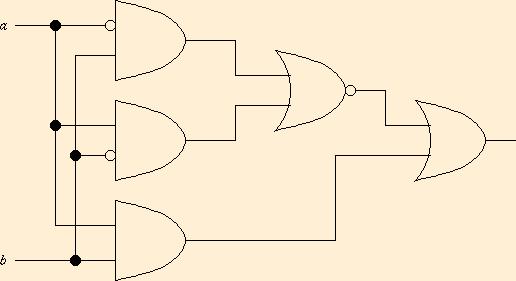
-
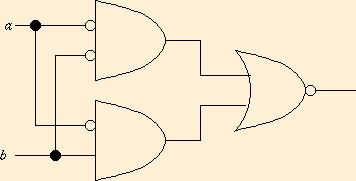
- Design a latch with only 3 binary gates: 2 ands and 1
or. You will need one invertor as well. (Just for fun,
speculate why the latch with 2 ands and 2 ors is more
popular.)
- Conversion to sum of products form may increase the size of a
Boolean expression exponentially, even after simplification. Show
how to construct, for each n, a Boolean expression with n
occurrences of variables whose sum of products form is exponential
in n.
- Wires in real electronic circuits have valued that vary
continuously between 0 and 1. Real circuits behave digitally
when they are reasonably sure to be at 0 or 1. Let
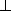 stand
for an unknown value between 0 and 1. Extend the operation tables
for and, or, inverse, mux to deal with
stand
for an unknown value between 0 and 1. Extend the operation tables
for and, or, inverse, mux to deal with
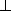 inputs in the most sensible way.
inputs in the most sensible way. - Based on your operation tables for 0,
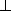 , 1, construct
a circuit with a loop that can produce output
, 1, construct
a circuit with a loop that can produce output 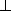 when all inputs
are 0 and 1. Such a state of a circuit is called ``metastable.''
Illustrate the behavior with graphs of the variation of inputs and
output.
when all inputs
are 0 and 1. Such a state of a circuit is called ``metastable.''
Illustrate the behavior with graphs of the variation of inputs and
output.
Several of the questions are taken from Dan Hyde's Web materials for
CCSCI320 at Bucknell University.
Com Sci 222/322
Assignment #1
Winter 1999
Boolean arithmetic and circuits
Due Wednesday 13 January
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 assignment_1.
The translation was initiated by Mike O'Donnell on Wed Jan 6 17:21:26 CST 1999
Mike O'Donnell
Wed Jan 6 17:21:26 CST 1999
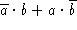 vs.
vs. 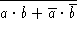
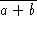 vs.
vs. 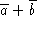
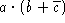 vs.
vs.